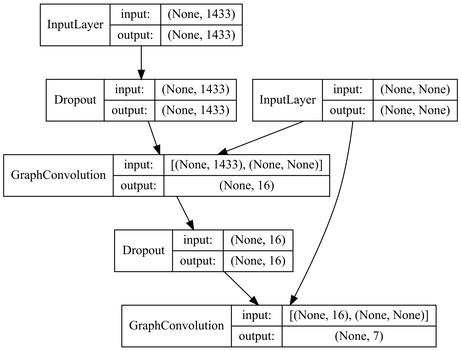
GraphAttentionNetworkのコード実装部分の入出力
https://github.com/danielegrattarola/keras-gat
実装部分の詳しい解説はこちらの説明がとても分かりやすい。
エッジごとに足し合わせる重みをAttentionと呼ばれる行列で代用するというもの。
Graph Convolutionを自然言語処理に応用する part2
ここに貼ってあった画像だけここに貼っておく。
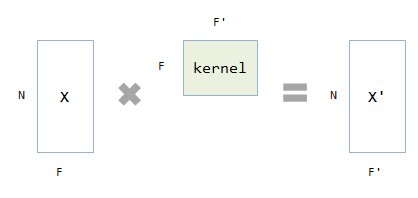
ノード表現に対する重みの乗算
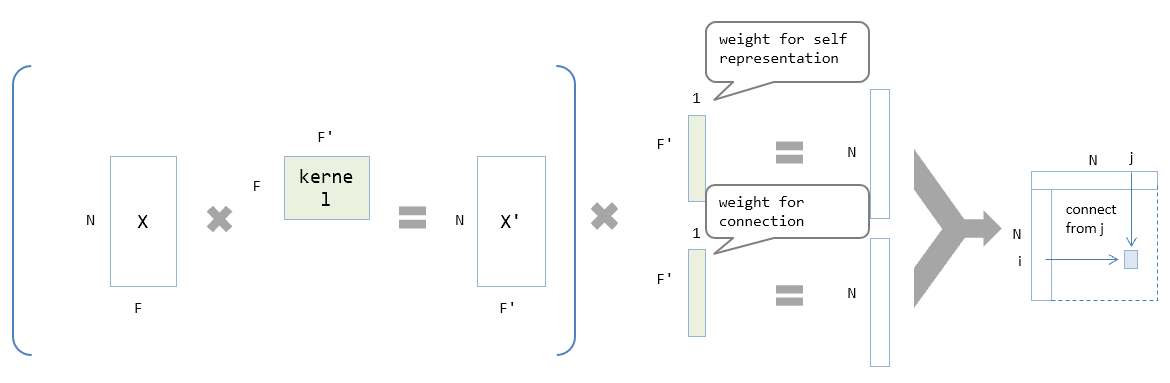
Attentionのベースとなる重みの計算

Attentionの計算
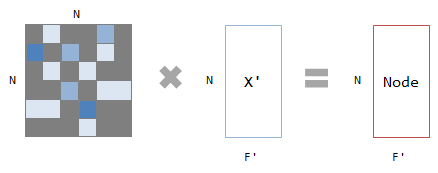

Attentionの適用
GraphAttentionNetworkが実装されているLayerへの入力は
ノードの数をN、ノード自信を表す特徴量の数をFとすると、
入力
- 隣接行列 A (形状はNxN。 Attention ではない)
- ノード自身の情報 X (NxF)
出力
新たに出力するノードごとの特徴量の数をF’とすると、
- 新しいノードの情報 Y (NxF’)
これから補完する必要のある部分
入力に対応している隣接行列の種類が1種類に限定されているため、エッジが表すことのできる関係性が1種類のみの状態となっているので、AMRが表す関係性の種類は100を超えてくるためこの部分は変える必要あり。
GraphConvolutionalNetworksのコード実装部分の入出力
一通りの説明は以下のURLにある。
https://omedstu.jimdo.com/2018/05/13/keras%E3%81%AB%E3%82%88%E3%82%8Bgraph-convolutional-networks/
入力
- 隣接行列 A (NxN)
- ノード自身の情報 X (NxF)
出力
- 新しいノードの情報 Y (NxF’)
出力の計算の仕方は以下の通り。
f(H^{(l)}, A) = \sigma(D^{-\frac{1}{2}}A’ D^{- \frac{1}{2}} H^{(l)}W^{(l)}) \\
ここで出現する
コード内ではGに相当する。
補完する必要のあるところ
こちらも隣接行列が多種類存在する場合に対応してない可能性が高い。
コードの理解不足かもしれないので試してみないと分からないが以下の画像を見る限りNxN(None x None)が入力になっているので恐らくできない。
右側のinput_layerが隣接行列Aで、左側が特徴行列のXとなっている。