GPyTorch Regression Tutorial

0. はじめに(前提)
1. モデル設定
- 1.1 GP Model
- 1.2 Modelのモード
2. モデルの訓練
3. モデルを使用した推論
4. モデルの一致度をプロットする

0. はじめに(前提)

以下の関数をモデリングする

$y = sin(2 \pi x) + \epsilon \\ \epsilon \sim \mathcal{N}(0, 0.04)$

必要モジュールのimport.

import math
import torch
import gpytorch
from matplotlib import pyplot as plt

%matplotlib inline 
%load_ext autoreload
%autoreload 2

# 訓練データの生成
train_x = torch.linspace(0, 1, 100)
train_y = torch.sin(train_x * (2 * math.pi)) + torch.randn(train_x.size()) * math.sqrt(0.04)

1. モデル設定

いくつか作成する方法がある

ガウス過程のフルモデルは提供しない。PyTorchでニューラルネットワークを構成するときの構成に似せており、柔軟性をもたせている。

GP Model (gpytorch.models.ExactGP) : 推論の大部分を扱う
尤度 (gpytorch.likelihoods.GaussianLikelihood ) : ガウス過程回帰で使われる尤度
平均 : 事前に与えられるガウス過程での平均。( gpytorch.means.ConstantMean() から始めることをおすすめする)
カーネル : ガウス過程での分散を定義する。まずはRBFカーネルから始めるのをおすすめする。 (gpytorch.kernels.ScaleKernel(gpytorch.kernels.RBFKernel())
多次元正規分布 (gpytorch.distributions.MultivariateNormal) : 多次元分布をこれで表現する

1.1 GP Model

__init__ メソッドでは訓練データと尤度を受け取る。これを受けて、forward メソッドを実行するために必要な共通オブジェクトを生成する。
forward メソッドでは $n\times d$ のデータである $x$ を受け取り、多次元正規分布における平均と分散である $\boldsymbol{\mu}(x), K_{xx}$ を返す

# 非常にシンプルなGP Modelを使用する

class ExactGPModel(gpytorch.models.ExactGP):
    def __init__(self, train_x, train_y, likelihood):
        super(ExactGPModel, self).__init__(train_x, train_y, likelihood)
        self.mean_module = gpytorch.means.ConstantMean()
        self.covar_module = gpytorch.kernels.ScaleKernel(gpytorch.kernels.RBFKernel())

    def forward(self, x):
        mean_x = self.mean_module(x)
        covar_x = self.covar_module(x)
        return gpytorch.distributions.MultivariateNormal(mean_x, covar_x)

# 尤度とモデルを初期化する
likelihood = gpytorch.likelihoods.GaussianLikelihood()
model = ExactGPModel(train_x, train_y, likelihood)

1.2 Modelのモード

ExactGP は .train() と .eval() モードを持っている。
ここは既存のpytorchと同様で、 .train()はハイパーパラメータの最適化時に使用され、 .eval() は推論時に使用される

2. モデルの訓練

GPyTorchでは、pytorchで使われているモジュールを一部流用する。
最適化の際は torch.optim を使用し、訓練対象のパラメータは torch.nn.Parameter 型とする必要がある。
これは、ガウス過程モデルが toch.nn.Module を直接拡張したものとなっているため、 model.parameters() や model.named_parameters() 関数のようにPyTorchのように関数を呼び出す。

訓練ループは以下の通り。

パラメータの勾配を全てゼロで初期化する
モデルを呼び出し、損失を計算する
誤差逆伝播を行う
optimizerのstep関数を呼び出す

しかしながら、訓練ループは非常に柔軟に定義することが可能である。

# これはNotebook用に呼び出している関数
import os
smoke_test = ('CI' in os.environ)
training_iter = 2 if smoke_test else 50

# 最適化対象のハイパーパラメータを見つける
model.train()
likelihood.train()

# adam optimizerを使用する
optimizer = torch.optim.Adam([
    {'params': model.parameters()},  # GaussianLikelihood のパラメータを含む
], lr=0.1)

# ガウス過程の損失 - 対数周辺尤度(the marginal log likelihood)
mll = gpytorch.mlls.ExactMarginalLogLikelihood(likelihood, model)

for i in range(training_iter):
    # 勾配をゼロにする
    optimizer.zero_grad()
    # モデルからの出力
    output = model(train_x)
    # 損失を計算し、勾配を逆伝播させていく
    loss = -mll(output, train_y)  # 尤度は最大化させたいのでここでは負の値として損失として扱う
    loss.backward()
    print('Iter %d/%d - Loss: %.3f   lengthscale: %.3f    noise: %.3f' %(
        i + 1, training_iter, loss.item(),
        model.covar_module.base_kernel.lengthscale.item(),
        model.likelihood.noise.item()
    ))
    optimizer.step()

3. モデルを使用した推論

eval モードの学習済みモデルは事後分布の平均と分散を返す。
以下のように、予測値を返すことができる。

f_preds = model(test_x)
y_preds = likelihood(model(test_x))

f_mean = f_preds.mean
f_var = f_preds.variance
f_covar = f_preds.covariance_matrix
f_samples = f_preds.sample(sample_shape=torch.Size(1000,))

# evaluation モードに変更
model.eval()
likelihood.eval()

with torch.no_grad(), gpytorch.settings.fast_pred_var():
    test_x = torch.linspace(0, 1, 51)
    observed_pred = likelihood(model(test_x))

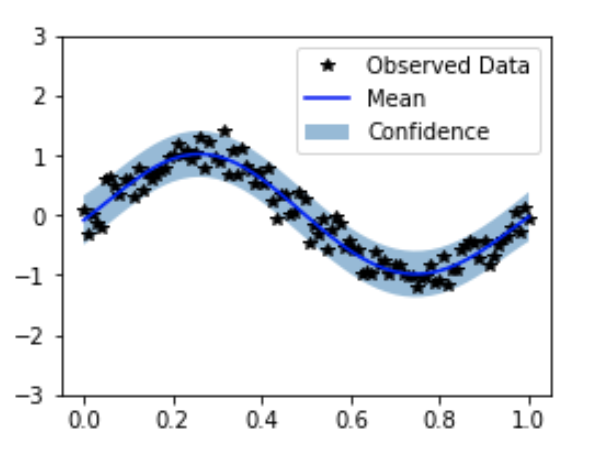
4. モデルの一致度をプロットする

最後に簡単に可視化をする。

# evaluation モードに変更
model.eval()
likelihood.eval()

with torch.no_grad(), gpytorch.settings.fast_pred_var():
    test_x = torch.linspace(0, 1, 51)
    observed_pred = likelihood(model(test_x))

Pocket