サポートベクターマシンまとめ

[mathjax] サポートベクターマシンについてほとんど理解していなかったのでこれを機会に色々理解していく。

サポートベクターマシン入門

上記のpdfを一通り読んでみたが行間を埋め切れることができなかったが一応イメージはつかめた気がする。

読んでみた感想としては、一番単純なニューラルネットワークとほとんど変わらない。

だった。

上の内容をそのまま写経してもただ日本語を写すだけなのであまり意味がない(自分が学習する意味合いとか記事としての需要も)ので、今回はscikit-learnの公式ページにある以下のページを一通り訳していこうと思う。
マジで訳しているだけ。意味が分からないものがあったら自分なりの解釈を入れるかもしれないが、基本的には原文どおり。

scikit-learnのツールの使い方もそのまま学ぶことができるので一石二鳥ということでscikit-learnの公式ドキュメントを選んだ。
物足りなかったらほかの英語サイトを訳すかもしれないけど、多分これで満足するのでちゃんと理解する。

わからない単語は逐一調べてはいるが、誤訳があったら教えてもらえると非常に助かります。

1.4. Support Vector Machines scikit-learn

以下で使ってる画像は上記のサイトから引用してきたもの。
サンプルコードは手元のIPythonを使って実行させたもの。
使っているものは以下の通り。

• OS: Windows10
• scikit-learn 0.19.2
• NumPy 1.14.5
• Scipy 1.1.0

導入

サポートベクターマシン(Support Vector Machines; SVMs)は教師あり学習 の手法としてクラス分けや回帰問題、そして外れ値検知(outlier detection)に使われている。

利点

サポートベクターマシンの利点としては以下の4点が挙げられる。

カーネル関数はサポートベクターマシンで境界面(線)を設定する多次元空間に写像する関数のこと。

• 高次元空間で有効
• 学習するデータ数よりもカーネル関数により写像される多次元空間の次元数の数のほうが多い場合にも効果的
• サポートベクター(support vectors)と呼ばれる、訓練集合の一部のデータを使って学習をする。そのため、メモリー効率も良い
• データとなるベクトルを多次元空間に写像するカーネル関数(主に内積など)を色々変えることが可能。これによりいろいろなモデルを構築でき、自らカーネル関数を設定することも可能。

欠点

欠点は以下の通り。

• 特徴量(入力されるベクトルの次元数)が訓練データの個数よりもかなり多い場合、過学習を防ぐため、カーネル関数の選択や正規化には慎重になる必要がある。
• サポートベクターマシンは境界面を設定するものなので、確率を計算することはしないため、５つに訓練データを分けて汎化性能を確かめるクロスバリデーションをする必要がある。クロスバリデーションはかなり計算コストが高い。

scikit-learnでは密なデータ(“numpy.ndarray”)や疎なデータ(“scipy.sparse”)を入力として使う。しかしながら、疎な予測データを計算するためにSVMを使うためには、その疎なデータをしっかりと学習する必要がある。より最適化された計算パフォーマンスを引き出したい場合、C-オーダーの”numpy.ndarray”や”scipy.sparse.csr_matrixをデータ型が”float64″で使うとよい。

クラス分け、分類(Classification)

SVCはSupport Vector Classificationの略で、分類問題の際に使われるSVMのこと。

SVC(一番一般的に使われるクラス分け用のSVM)、NuSVC(使うサポートベクターの数を制限したSVC)、LinearSVC(カーネル関数に線形関数を使うクラス分け用のSVM)は、複数クラスに分類するためのscikit-learnのclassである。

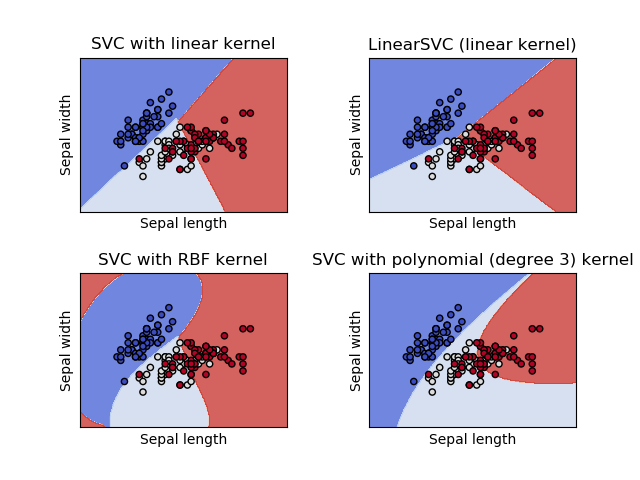
それぞれのscikit-learnのクラスでIris-dataを分類したようす。

SVCとNuSVCは似ているが、若干異なったパラメータ群を用い、異なった数学的手法をつかっている(数学的手法の節参照)。

一方で、LinearSVCはカーネル関数が線形のときに使うSupport Vector Classificationの実装である。
LinearSVCは”kernel=’linear'”で固定なため他のカーネル関数に設定することができないことに注意が必要。また、他の”support_”引数といったSVCやNuSVCには含まれているが、LinearSVCには含まれていない引数がある。

他の分類関数と同様、これら3つのメソッドは入力データとして2つの配列を指定する。
Xは[サンプル数(n_samples),特徴量数(n_features)]の形状を持つ訓練データでyはラベルデータで、[n_samples]の形状を持つ。

In [1]: from sklearn import svm

In [3]: import numpy as np

In [4]: X = np.array([[0,0],[1,1]])

In [5]: y = np.array([0,1])

In [6]: clf = svm.SVC()

In [7]: clf.fit(X,y)
Out[7]:
SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape='ovr', degree=3, gamma='auto', kernel='rbf',
max_iter=-1, probability=False, random_state=None, shrinking=True,
tol=0.001, verbose=False)

これでフィッティングができたので、新たなデータを入れてその値を予測させてみる。

In [8]: clf.predict([[2.,2.]])
Out[8]: array([1])

単純に使うだけならこれだけで使えてしまうからかなり便利。

SVMsの分類関数はサポートベクターと呼ばれる、訓練データの部分集合に依拠している(ただ一部の条件に合致する訓練データをそう呼んでるだけ)。
サポートベクターの概要は”support_vectors_”,”support_”そして”n_support”属性(attribute)で知ることができる。

In [9]: clf.support_vectors_ # サポートベクターの表示
Out[9]:
array([[0., 0.],
[1., 1.]])

In [10]: clf.support_ # サポートベクターのインデックス(順番)を表示
Out[10]: array([0, 1])

In [11]: clf.n_support_ # それぞれのクラスに使われているサポートベクターの数
Out[11]: array([1, 1])

複数クラスへの分類

SVCやNuSVCは多クラス用の”1対1″(one-against-one)(Knerr et al., 1990)の手法を使っている。
2つのクラスのうちどちらかを判別 する手法である。

“n_class”がクラスの数だとすると、
n_{classifier} = \frac{n_{class}(n_{class}-1)}{2}
で求められる”n_classifier”個分だけ分類器(“classifier”)が作られ、それぞれの分類器は2つのクラスからデータを学習する(恐らく1つの分類器は特定の2つのクラスに分けるための分類器であるということだと思う)。
他の分類器と衝突を起こさないために、”decision_function_shape”引数を指定することで、”one-against-one”分類器の結果を、”(n_samples, n_classes)”の形状を持つ分類関数に変換することができる。

In [12]: X = np.array([[0],[1],[2],[3]])

In [13]: Y = np.array([0,1,2,3])

In [14]: clf = svm.SVC(decision_function_shape='ovo') # 分類器による出力は"one-vs-one"で1対1手法を使う

In [15]: clf.fit(X, Y)
Out[15]:
SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape='ovo', degree=3, gamma='auto', kernel='rbf',
max_iter=-1, probability=False, random_state=None, shrinking=True,
tol=0.001, verbose=False)

In [17]: dec = clf.decision_function([[1]])

In [18]: dec.shape[1] # 4つクラスがあるので 4*3/2 = 6より6つ分類器が存在する
Out[18]: 6

In [19]: clf.decision_function_shape = "ovr" # 1対他(on-vs-rest)

In [20]: dec = clf.decision_function([[1]])

In [21]: dec.shape[1]
Out[21]: 4

一方で、LinearSVCは”one-vs-the-rest”(1対残り)を使った複数クラスの分類手法を使っている。そのため、1つのクラスなのかそれ以外なのかを判定 する分類器を作るということなので、クラスの数分だけ分類器を生成すればよい。2クラス分類問題であれば、モデルは1つだけしか生成されない。

In [22]: lin_clf = svm.LinearSVC()

In [23]: X
Out[23]:
array([[0],
[1],
[2],
[3]])

In [24]: Y
Out[24]: array([0, 1, 2, 3])

In [25]: lin_clf.fit(X,Y) # フィッティング
Out[25]:
LinearSVC(C=1.0, class_weight=None, dual=True, fit_intercept=True,
intercept_scaling=1, loss='squared_hinge', max_iter=1000,
multi_class='ovr', penalty='l2', random_state=None, tol=0.0001,
verbose=0)

In [26]: dec = lin_clf.decision_function([[1]]) # 分類器の関数

In [27]: dec.shape[1]
Out[27]: 4

分類器については数学的手法のところで詳説する。

LinearSVCはCrammerとSingerらによって提唱されたmulti-class SVM(他クラスSVM)と呼ばれるもう１つの他クラス分類のための手法もカバーしている。この手法は”multi_class=’crammer_singer'”と指定することで使用可能である。
この手法はデフォルトで設定されている”one-vs-rest”で起こりえた他の分類器と衝突がない。
実践の場において、’crammer_singer’と比べて通常出力が変わらず計算時間が非常に少ないため”one-vs-rest”(1対他)の方が好ましい。

“one-vs-rest”を使うLinearSVCでは、”coef_”と”intercept_”属性(attributes)はどちらも”[n_class, n_features]”の形状を持つ。係数の各行は”n_class”個もあるたくさんの”one-vs-rest”分類器や切片(intercepts)に一致しており、”one”のほうの順番にそって並べられている。

SVCの”one-vs-one”(1対1)の場合、属性(attributes)のレイアウトは若干変化してくる。線形のカーネル関数を使ている場合、”coef_”、”intercept_”属性のレイアウトは先ほど説明したLinearSVCのものと似ている。相違点としては”coef_”の形状が
[\frac{n_{class} (n_{class}-1)}{2}, n_{features}]
と2クラス分類器の集まりのものと一致する。クラスの順番としては”0と1″,”0と2″…,”0とn”,…”n-1とn”のように続いている。

“dual_coef_”の形状は”[n_class-1, n_SV]”(n_SVはサポートベクターの数)であり、概要を把握するのが難しい。列は”n_class*(n_class-1)/2″個ある”one-vs-one”(1対1)分類器のうちのどれかに関するサポートベクターに対応している。それぞれのサポートベクターは”n_class-1″分類器に使用される。”n_class-1″個もの行はその分類器の二重係数(dual coefficient)となっている。
(サポートベクターとそれぞれのクラス分類に使われてるものとの関係を示してるということだと思う。ここは理解をしていく必要がありそう。)

手元で出力させてみたところ以下のようになった。

In [1]: from sklearn import svm

In [2]: import numpy as np

In [3]: X = [[0],[1],[2],[3]]

In [4]: Y = [0, 1, 2, 3]

In [5]: clf = svm.SVC(decision_function_shape='ovo')

In [6]: clf.fit(X,Y)
Out[6]:
SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape='ovo', degree=3, gamma='auto', kernel='rbf',
max_iter=-1, probability=False, random_state=None, shrinking=True,
tol=0.001, verbose=False)

In [7]: clf.dual_coef_
Out[7]:
array([[ 1., -1., -1., -1.],
[ 1.,  1., -1., -1.],
[ 1.,  1.,  1., -1.]])

これは例でみていくと分かりやすいだろう。

3クラス分類問題を考えてみる。クラス0は3つのベクトル
v_0^0, v_0^1, v_0^2 \
を持っており、クラス1,2はそれぞれ2つのベクトル
v_1^0, v_1^2 \
v_2^0, v_2^1 \
それぞれのベクトル
v_i^j \
は2つの二重係数(dual coefficients)が存在する。

ここでクラスi,kの分類器に使われるサポートベクターv_i^jの係数を
\alpha_{i,k}^j \
とする。

このとき、”dual_coef_”は以下のようになる。

ここでCoefficientsは係数を示している。

それぞれのサポートベクターにかかる係数を示していることになる。

評価と確率

SVCの”decision_function”メソッドはそれぞれのサンプルのクラスあたりのスコアを表示する(もしくは2クラス分類の場合は1つのサンプルあたりに単独のスコアが表示される)。SVCクラスを作るときに”probability”引数を”True”にしておくと、”predict_proba”と”predict_log_proba”メソッドを呼び出すことでクラスごとの確立を計算することができる。2クラス分類の場合、確率はPlattスケーリングと呼ばれる手法によって調整される。Plattスケーリングとは、訓練データのクロスバリデーションによって学習したSVMのスコアを使ってロジスティック回帰を行うことである。複数クラス分類問題の場合、2クラス分類で使われた調整法を拡張することになる(Wu et al.(2004)参照)。

言うまでもないことだが、Plattスケーリングにおけるクロスバリデーションは巨大なデータセットを使った計算コストのかかる処理である。それに加え、計算された確率はスコアと矛盾することがあり得る。スコアの最大値を示すデータが確立の最大値となっているとは限らないからだ。例えば、2クラス分類問題のとき、データごとに”predict”の値によってラベル付けが施されるが”predict_proba”で計算されるそのクラスに属する確率が1/2以下になることが起こりうる。Plattが提唱する手法は理論的な問題を抱えていることでも知られている。もし、信頼度のスコアを求める必要があるが確率を求める必要がない場合、”probability=False”にし、”predict_proba”を”decision_function”の代わりに使うことをオススメする。

参照
– Wu, Lin and Weng, Probability estimates for multi-class classification by pairwise coupling, JMLR 5:975-1005, 2004.
Platt [Probabilistic outputs for SVMs and comparisons to regularized likelihood methods] (http://www.cs.colorado.edu/~mozer/Teaching/syllabi/6622/papers/Platt1999.pdf).

偏りのあるデータセットへの対応

特定のクラスや特定のサンプルにたいして重みづけをつけて重要度を増したいときは”class_weight”や”sample_weight”が使える。

SVC(NuSVCではない)では”class_weight”引数を”fit”メソッドで実装している。”{class_label : value}”({クラスのラベル:値})(valueは0より大きい浮動小数(float))で指定でき、それによりクラスごとのパラメーター”C”を”class_label”から”C*value”に変換する。

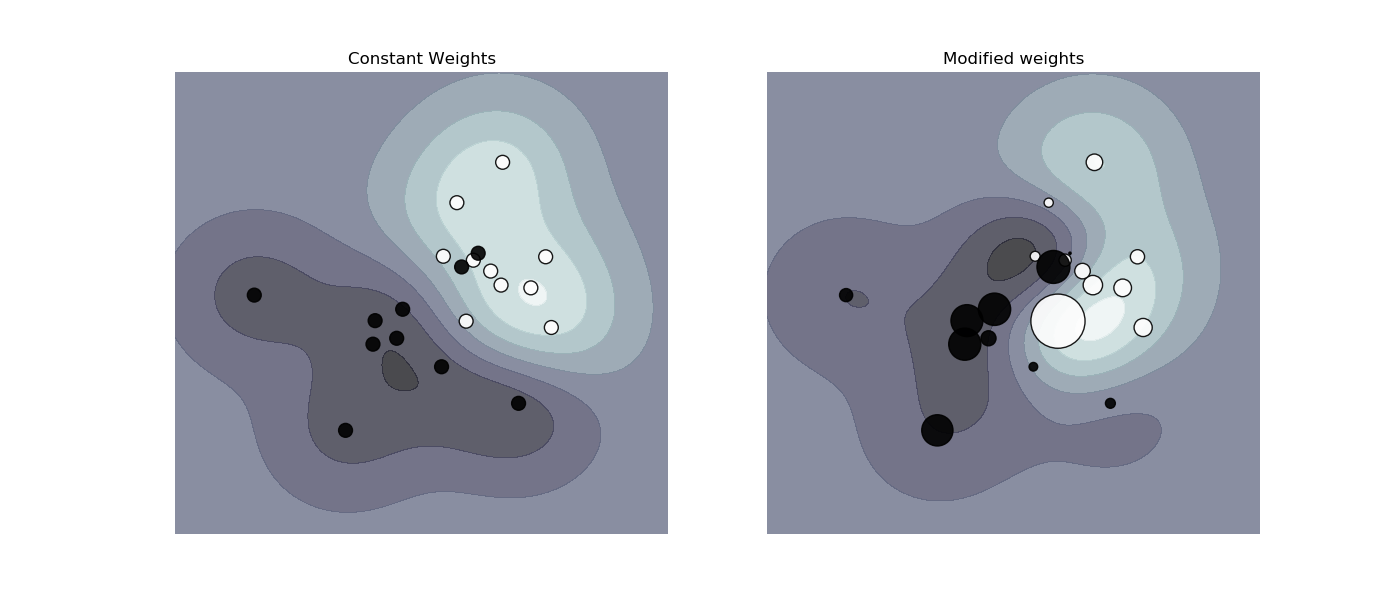
以下のグラフはサンプル数に偏りのあるサンプルに重みをつけることでより境界を正しく推定できるようになった例である。

SVC,NuSVC,SVR,NuSVR,OneClassSVMは”fit”メソッドの中に”sample_weight”を指定することで各々のサンプルに対して重みづけをすることができる。”class_weight”に似て、これらはi番目のサンプルのパラメーター”C”を”C*sample_weight[i]”にする。

例
– Plot different SVM classifiers in the iris datset,
– SVM: Maximum margin separating hyperplane,
– SVM: Separating hyperplane for unbalanced classes
– SVM-Anova: SVM with univariate feature selection,
– Non-linear SVM,
– SVM: Weighted samples

回帰

Support Vector Classificationのメソッドは回帰問題にまで拡張することが可能。Support Vector Regression(SVR)と呼ぶ。

境界線の付近に存在しない訓練データは損失関数に含まれないため、SVCによるモデルは一部の訓練データに依拠した形になる。同様に、Support Vector Regressionによって生成されたモデルは損失関数にモデルが予測した値に近い訓練データをすべて含まないため、一部の訓練データに依拠する。

scikit-learnにはSupport Vector Regressionの3つの実装がある。
– SVR,
– NuSVR,
– LinearSVR,

LinearSVRはSVRよりも高速に最適化するが線形カーネルしか扱わない。一方でNuSVRはSVRやLinearSVRとは若干異なった手法を実装している。詳しくは数学的手法を参照。

クラス分けのクラスでは、X,yを引数としてフィッティングをする。yは整数ではなく浮動小数の値を持ったベクトルとなる。

In [1]: from sklearn import svm

In [2]: X = [[0,0],[2,2]]

In [3]: y = [0.5, 2.5]

In [4]: clf = svm.SVR()

In [5]: clf.fit(X,y)
Out[5]:
SVR(C=1.0, cache_size=200, coef0=0.0, degree=3, epsilon=0.1, gamma='auto',
kernel='rbf', max_iter=-1, shrinking=True, tol=0.001, verbose=False)

In [6]: clf.predict([[1,1]])
Out[6]: array([1.5])

例
– Support Vector Regression(SVR) using linear and non-linear kernels

密度の推定と新規性の検知

One-class SVMは新規性の検知に使われる。新しいデータを既存のグループに属しているのかどうかを判別するために境界線をソートする。これを実装したものがOneClassSVMである。
(このあたりの訳が自信ない)

このような教師なし学習の場合、フィティングメソッドでは入力ベクトルはXだけをとり、ラベルデータは存在しない。

詳しくはこちらを参照してほしい。

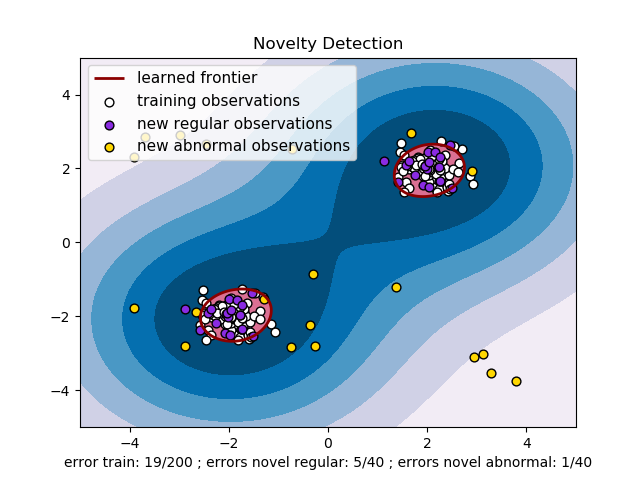
例
– One-class SVM with non-linear kernel(RBF)
– Species distribution modeling

難点

サポートベクターマシンは強力なツールだが、訓練データの数が増えるにつれて急激に計算量やメモリの容量が増加していく。SVMの核となっている部分は二次計画法(quadratic programming problem;QP)であり、サポートベクターと他の訓練データとを仕分けする。libsvmを基盤とする実装に使われているQPソルバーはO(n_{features}\times n^2_{samples})とO(n_features\times n^3_{samples})の間に大きさを整える。これはlibsvmが実際にほどキャッシュの中で効率よく使われているかに依存する。もしデータが非常に疎(sparse)であった場合、n_{features}はサンプルベクトルの非ゼロ特徴量の平均個数に置き換わる。

線形の場合、liblinearの実装がされているLinearSVCで使われているアルゴリズムはlibsvmベースのSVCの線形カーネルのものよりも計算効率が良く、何百万ものデータ数や特徴量を線形にスケール化できる。

カーネル関数

カーネル関数は以下のような形をとりうる。

• 線形
  $$<x,x’> \\$$
• 多項式 dは”degree”引数によって指定。rは”coef0″。
  (\gamma <x, x’> + r)^d
• rbf(Radial Basis Function;放射基底関数) γ(>0)は”gamma”引数により指定。
  exp(-\gamma||x-x’||^2)
• sigmoid rは”coef0″により指定。
  tanh(\gamma<x,x’> + r)

他のカーネル関数は初期化の際”kernel”引数により指定できる。

In [1]: from sklearn import svm

In [2]: linear_svc = svm.SVC(kernel='linear')

In [3]: linear_svc.kernel
Out[3]: 'linear'

In [4]: rbf_svc = svm.SVC(kernel='rbf')

In [5]: rbf_svc.kernel
Out[5]: 'rbf'

カーネル関数を自作する

Pythonの関数をカーネル関数として指定したり、グラム行列をあらかじめ計算しておくことでカーネルを指定することができる。

自作したカーネルを持つ分類器は以下の点を除いて他の分類器と同様に扱える。
– “support_vectors_”フィールドが空白(empty)となり、サポートベクターのインデックスが”support_”フィールドの中でしか保存されない。
– fitメソッドの第一引数への参照がのちに参照されるために保存される。”fit”と”predict”メソッドの使用でその配列が変化してしまう場合、予期しない結果を得ることになる。

カーネルとしてPythonの関数を使う

SVCオブジェクトを作る際”kernel”引数に関数を指定することで自分で定義した関数をカーネル関数として使うことができる。

カーネル関数の中で、
(n_{samples}^1, n_{features}), (n_{samples}^2, n_{features}) \
の形状を持つ行列をパラメーターにとり、返り値は
(n_{samples}^1, n_{samples}^2) \
の形状を持つ行列となるようにしなければならない。

以下のコードでは線形のカーネルを定義し、それを使って分類器を作っている。

In [6]: import numpy as np

In [7]: from sklearn import svm

In [10]: def my_kernel(X,Y):
...:     return np.dot(X, Y.T)
...:
...:

In [11]: clf = svm.SVC(kernel=my_kernel)

例
– SVM with custom kernel

グラム行列を用いた例

“kernel=’precomputed'”にし、”fit”メソッドの中でグラム行列をXの代わりに渡す。この時、全ての訓練データのベクトルとテストデータのベクトルのカーネルの値が分かっている必要がある。

In [32]: import numpy as np

In [33]: from sklearn import svm

In [34]: X = np.array([[0,0],[1,1]])

In [35]: y = [0,1]

In [36]: clf = svm.SVC(kernel='precomputed')

In [38]: gram = np.dot(X, X.T)

In [39]: clf.fit(gram, y)
Out[39]:
SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape='ovr', degree=3, gamma='auto',
kernel='precomputed', max_iter=-1, probability=False, random_state=None,
shrinking=True, tol=0.001, verbose=False)

In [40]: clf.predict(gram)
Out[40]: array([0, 1])

RBFカーネルでのパラメータ

Radial Basis Function(放射基底関数)カーネルのあるSVMを学習させるとき、”C”と”gamma”の2つのパラメーターを考慮に入れる必要がある。”C”は全てのSVMカーネルに共通で、誤って分類した訓練データを決定面の単純さに逆らって置き換える。低い値の”C”は決定面を滑らかにし、高い値の”C”はより多くの訓練データを正しく分類しようとする。”gamma”は1つの訓練データをどれほど重要視するかを決める。”gamma”の値が大きいほど、より他のデータが影響を受けて近くなる。

“C”と”gamma”を適切に選ぶことはSVMのパフォーマンスを向上させるうえで必須である。”sklearn.model_selection.GridSearchCV”を”C”と”gamma”で指数的に値をとって試してみて適切な値を選び取ることをおすすめする。

例
– RBF SVM parameters

数学的手法

サポートベクターマシンは分類や回帰などに使える超平面(hyper-plane)か超平面の集合を高次元、もしくは無限高次元空間に作り出す。直感的には、好ましい分割は最も近くにあるどのクラスに属する訓練データのポイントからも最も離れている超平面を作り出すことである。これは、一般的により大きいマージン(余白、距離)を作ったほうが分類器を一般化する際の誤差を少なくするからだ。

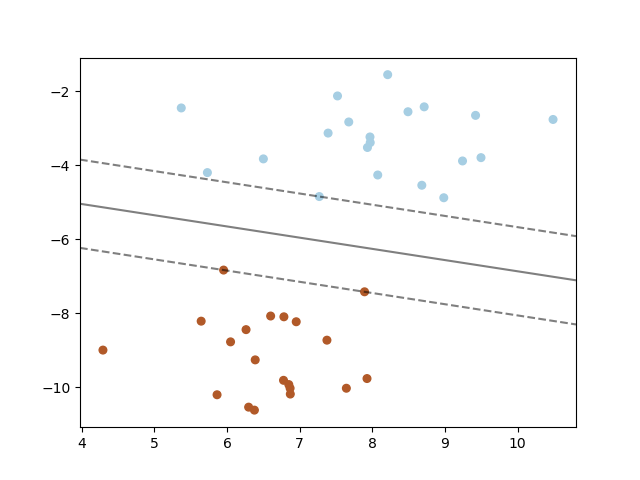
ちなみにマージンの距離は

\frac{1}{||w||} \

で求めることができるので、基本的にはこれの値を最大化したいのが目標であるため、逆数をとって、

\frac{1}{w^Tw}

の値を最小化するのが大まかな学習の目的だ。

SVC(Support Vector Classifier)

訓練データとして以下のベクトル群が与えられてるとき、

\vec{x}_i \in \mathcal{R}^p \
(i = 1, 2,\cdots, n) \

があり、教師ベクトル群

\vec{y} \in {1, -1}^n \

があったとして、以下のような拘束条件の下、

y_i(w^T \phi(\vec{x}_i) + b ) \geq 1 – \zeta_i \
\zeta_i \geq 0, i = 1,\cdots,n \

以下の値

\frac{1}{2}w^Tw + C \sum^n_{i=1} \zeta_i \

を最小化する

w, b, \vec{\zeta}

の値を求める。

これは以下のような条件に置き換えることができる。

\vec{y}^T \vec{\alpha} = 0 , 0 \leq \alpha_i \leq C, i = 1, \cdots, n \
の条件のもと
\frac{1}{2}\vec{\alpha}^TQ\vec{\alpha} – e^T \vec{\alpha} \
を最小化するような
\vec{\alpha}
の値を見つければよい。ここで
e
は要素がすべて1のベクトルで、
C>0
は値の上限、
Q

はnxnの半正定値行列であり、

Q_{ij} \equiv y_iy_jK(\vec{x}_i,\vec{x}_j) \
(K(\vec{x}_i, \vec{x}_j) = \phi(\vec{x}_i)^T\phi(\vec{x}_j)はカーネル)

で定義される。
関数φによって訓練ベクトルは高次元空間に写像することになる。
分類関数は以下のとおりである。

sgn(\sum^n_{i=1}y_i\vec{\alpha}_i K(\vec{x}_i,\vec{x}) + \rho) \

ノート

libsvmとliblinearから使われているSVMモデルがパラメータCを正規化パラメータとして利用しているとき、他のほとんどの計算においてアルファが使われる。２つのモデル間で正規化する度合いがちょうど等価になることはモデルによって最適化された目的関数に依拠する。例えば、予測モデルとして”sklearn.linear_model.Ridge回帰が使われたとすると、Cとαの関係は以下のようになる。

C = \frac{1}{\alpha}\

“dual_coef_”でアクセスできる値は

y_i\alpha_i

であり、”intercept_”はρである。

参考
– Automatic Capacity Tuning of Very Large VC-dimension Calssifiers, I. Guyon, B. Boser, V. Vapnik – Advances in neural information processing 1993.
– Support-vector networks, C. Cortes, V. Vapnik – Machine Learning, 20, 273-297 (1995).

NuSVC

新しいパラメーターνを導入する。これはサポートベクターの数と訓練時の誤差を調整する役割を果たす。パラメーター

\nu \in (0, 1] \

は訓練時の誤差とサポートベクターの比の下限との比の上限となっている。

ν-SVCはC-SVCのパラメーターの値を振りなおしたのと数学的には等価である。

SVR

訓練ベクトル

\vec{x}_i \in \mathcal{R}^p \
(i = 1, \cdots, n) \

と教師ベクトル

\vec{y} \in \mathcal{R}^n \

が与えられたとき、ε-SVRは以下の問題を解く。

拘束条件として以下のものが与えられる。

y_i – w^T \phi(\vec{x}_i) – b \leq \varepsilon + \zeta_i \
w^T\phi(\vec{x}_i) + b – y_i \leq \varepsilon + \zeta_i^{\ast} \
\zeta_i, \zeta_i^{\ast} \geq 0, i=1,\cdots , n \

これは、予測時の誤差がある一定の範囲を超えないことを示してる。

このとき、以下の値の最小値を取るような

w, b, \zeta, \zeta^{\ast} \
の値を求める。

\frac{1}{2}w^Tw + C \sum_{i=1}^n (\zeta_i + \zeta_i^{\ast}) \

これは以下の問題の置き換えられる。

拘束条件

e^T(\vec{\alpha} – \vec{\alpha}^{\ast} = 0 \
0 \leq \alpha_i, \alpha_i^{\ast} \leq C, i=1,\cdots, n \

のもとで
以下の値を最小値とするような

\vec{\alpha}, \vec{\alpha}^{\ast} \

を求める。

\frac{1}{2}(\vec{\alpha} – \vec{\alpha}^{\ast})^TQ(\vec{\alpha}-\vec{\alpha}^{\ast}) + \varepsilon \varepsilon^T(\vec{\alpha} + \vec{\alpha}^{\ast}) – \vec{y}^T(\vec{\alpha} – \vec{\alpha}^{\ast}) \

eは要素が全て1のベクトルで、C>0は上限、Qはnxnの半正定値行列であり、その各要素は

Q_{ij} \equiv K(\vec{x}_i, \vec{x}_j) = \phi(\vec{x}_i)^T\phi(\vec{x}_j) \

となっており、これらがカーネルとなっている。関数φによって訓練ベクトルは高次元空間に写像される。

決定関数は以下の通りSVCとは異なり、符号をとらずそのままの値が出力になる。

\sum^n_{i=1}(\alpha_i – \alpha_i^{\ast})K(\vec{x}_i,\vec{x}) + \rho \

“dual_coef_”で

\alpha_i – \alpha_i^{\ast} \

の値を見ることができ、

“intercept_”で

\rho

の値を見ることができる。

参考
– A tutorial on Support Vector Regression,Alex J. Smola, Bernhard Schölkopf – Statistics and Computing archive Volume 14 Issue 3, August 2004, p. 199-222.

実装の詳細

内部の実装ではlibsvmとliblinearを使って計算を実行している。これらのライブラリーはC言語やCythonで実装されている。

参照
実装の詳細は以下のリンクから
– LIBSVM: A Library for Support Vector Machines.
– LIBLINEAR – A Library for Large Linear Classification.

まとめ

今回はscikit-learnの公式ドキュメントにあるサポートベクターマシンの部分を訳していく形でまとめた。

サポートベクターマシンはクラス分類では1つのサポートベクターでは2クラス分類しかできないのでいくつかの分類器を組み合わせて分類を行っている。

リグレッションでは誤差の上限をζであらわし、誤差を一定の範囲におさめながらマージンを最大化するように学習していく。

数学的なものが分かっていると、実装部分でアクセスできる値の意味合いもわかってくる。

かなり長くなってしまったが、一通り訳すことができたはず。もし間違いあったら教えてほしい。