ラッソ(Lasso)回帰とリッジ(Ridge)回帰をscikit-learnで使ってみる

投稿日投稿者leck_33281件のコメント

このエントリーをはてなブックマークに追加
Pocket

前回は線形回帰の最も基礎的な回帰手段である最小二乗法を扱った。
最小2乗法(OLS)をSCIKIT-LEARNで使ってみる
ここでは以下の損失項を最小にするようなパラメータwの組を求めた。
$$
|Xw-y|^2
$$
今回は手元にある訓練データを過剰に学習してしまうオーバーフィッティング(過学習)を防ぐための工夫の1つとして、損失項の中にパラメータの値の大きさを制限するものを入れるものがある。
その中でもパラメータベクトルのノルムの1乗を損失に加えるラッソ(Lasso)回帰とリッジ(Rdige)回帰について数式面で簡単にさらったあと、scikit-learnで実際に使ってみる。
今回も以下のscikit-learnの公式サイトを参考にしながらまとめた。
1.1 Generalized Linear Models — scikit-learn
それぞれの回帰の特徴としては
  • リッジ回帰
    パラメータの値が増大するのを防ぐことでオーバーフィッティングを防ぐ。
  • ラッソ回帰
    モデルに使う特徴量(説明変数)の数を減らすことでオーバーフィッティングを防ぐ。

リッジ(Ridge)回帰

定式化

リッジ回帰ではパラメータwの値が大きくなりすぎないように(生成されるモデルの形が歪になりすぎないように)パラメータのノルムの2乗(L2ノルム)を損失Lの値に加える。
$$
L = |Xw – y | ^2 + \alpha |w|^2
$$
ここでXはNxpの行列で、p個を1つのセットにしたデータをNセット分格納した行列(pは特徴量の数)。
yはN次元の縦ベクトルで教師データ。
$$
w = (w_1, w_2, \cdots, w_p)
$$
が今回推定したいパラメータ。
$$
\hat{y} = Xw + const \
$$
のモデルを構築するのが最終目標。
Lの値が最小になるようなパラメータwを求める。
ここのαは正則化項と二乗誤差との相対的な重要度を調節するハイパーパラメータなので、手動で調節するところ。
$$
\hat{w} = \underset{w}{argmin} L \
= \underset{w}{argmin} |Xw – y | ^2 + \alpha |w|^2
$$
Lをwについて偏微分した値が0になるような値を計算すると
$$
\frac{\partial L}{\partial w} = 2X^T(Xw-y) + 2\alpha w = 0 \ $$
w = (X^TX + \alpha E)^{-1}X^Ty \
$$
Eはp x pの単位行列。
これを見ると、逆行列を求めやすくなるように単位行列のα倍したものを足し合わせている。

実装

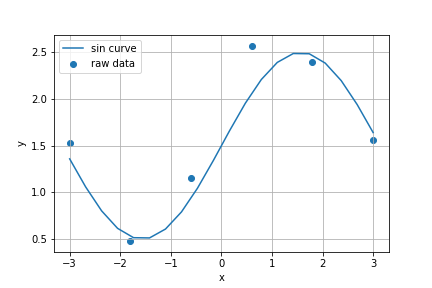
まずは学習させる元のデータを作成する。

import numpy as np
from sklearn import linear_model

np.random.seed(42)
N = 6 # サンプル数
x = np.linspace(-3, 3, N)
X = np.zeros((N,5)) # x, x^2, x^3, x^4, x^5を作る
X[:, 0] = x
for i in range(4):
    X[:,i+1] = X[:, i] * X[:, 0]
y = np.sin(X[:,0]).reshape(-1,1) + np.random.randn(N,1)/3.0 + 1.5
# 1.5が定数項
このデータをプロットすると以下のような感じ。

import matplotlib.pyplot as plt
xx = np.linspace(-3,3,20)
plt.scatter(X[:,0], y, label='raw data')
plt.plot(xx, np.sin(xx)+1.5, label='sin curve')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid()
plt.show()
これを以下のモデルで学習させる。
$$
y = w_0 + w_1x + w_2x^2 + w_3x^3 + w_4x^4 + w_5x^5 \ $$
w = (w_0, \cdots, w_5) \
$$
今回、変数はxのべき乗のみにした。 早速学習させる。

reg= linear_model.Ridge(alpha=10)  
reg.fit(X, y)
ols = linear_model.LinearRegression()  # 比較用
ols.fit(X, y)
結果をプロットする。

for i in range(4):
   XX[:, i+1] = XX[:,i]*XX[:,0]
print("α=0.5")
print("w_0 is \n", reg.intercept_)
print("w_1, w_2, w_3, w_4, w_5 is \n", reg.coef_)
plt.scatter(X[:,0], y, label='raw data')
plt.plot(xx, np.sin(xx)+1.5, label='sin curve')
plt.plot(XX[:,0], reg.predict(XX), label='trained model(rdige α=10)')
plt.plot(XX[:,0], ols.predict(XX), label='trained model(ols)')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid()
plt.show()
実行結果

α=0.5
w_1, w_2, w_3, w_4, w_5 is
 [[ 0.12737017 -0.05621336  0.15503859  0.00353578 -0.01866049]]
w_0 is
 [1.74259826]

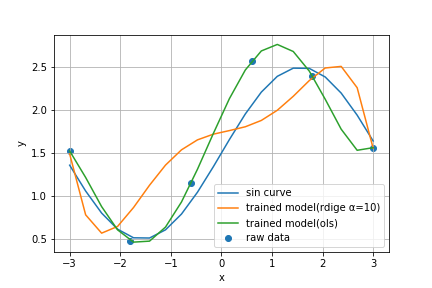
少ない点の数でもパラメータの値を抑制できるのでただの最小２乗法(OLS)よりも程よく近似できていることが分かる。
学習されたパラメータは以下の感じ。
モデルw_0w_1w_2w_3w_4w_5
Ridge(α=0.5)1.740.127-0.0560.1550.003-0.018
OLS1.9371.283-0.216-0.2820.0190.015
パラメータの絶対値が抑制されているのが分かる。

αの値を決める

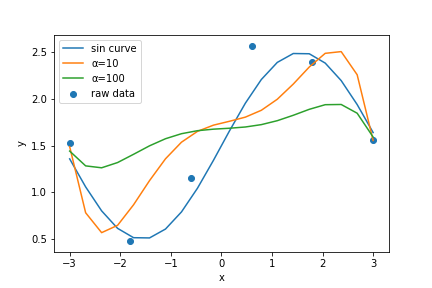
αの値を勝手に決めてもらうことも可能。
RidgeCVを使えば交差検証(cross validation)を使って丁度良いαの値を指定することができる。

reg_cv = linear_model.RidgeCV(alphas=[0.1, 1, 10, 100], cv=5)
reg_cv.fit(X, y)
print("alpha = ", reg_cv.alpha_)



alpha =  100

ラッソ(Lasso)回帰

定式化

ラッソ(Lasso)ではパラメータのノルムの1乗の項(L1ノルム)が損失に付け加えられる。
$$
L = \frac{1}{2n_{samples}}|Xw-y|^2 + \alpha|w| \
$$
サンプル数で二乗誤差を正規化しているがリッジ回帰との本質的な違いはL2ノルムではなくL1ノルムだけが付け加わっていること。
この形の損失だとαの値が十分に大きければwの成分の一部が0になり、疎な解(有効な特徴量の数が少ないモデル)を得られる。
αの値で正則化の度合いを調整する。

変数選択をする基準

Lasso回帰は回帰に使用する変数を減らす目的で使われるので、その変数を選択する基準をいくつか用意している。
  • AIC(赤池情報量基準; Akaike information criterion)
  • BIC(ベイズ情報量基準; Beyesian information criterion)

実装

先ほどのサインカーブの予測を行う。

reg_lasso = linear_model.Lasso(alpha=0.1)
reg_lasso.fit(X,y)
モデルw_0w_1w_2w_3w_4w_5
OLS1.9371.283-0.216-0.2820.0190.015
Lasso(α=0.1)1.710.575-0.0290.00.001-0.007
Ridge(α=0.5)1.740.127-0.0560.1550.003-0.018
変数が選択されていることが分かる。
学習させたモデルを可視化してみる。

XX = np.zeros((20,5))
XX[:,0] = xx
for i in range(4):
    XX[:, i+1] = XX[:,i]*XX[:,0]


plt.scatter(X[:,0], y, label='raw data')
plt.plot(xx, np.sin(xx)+1.5, label='sin curve')
plt.plot(xx, reg_lasso.predict(XX), label='lasso(α=0.1)')
plt.xlabel('x')
plt.ylabel('y')
plt.grid()
plt.legend()
plt.show()

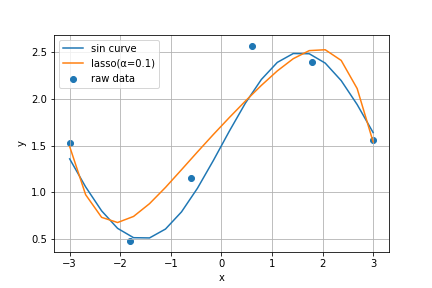
かなり程よく近似されてるのが分かる。
今回のケースではリッジ回帰よりもラッソ回帰の方がうまく回帰できたようだ。

交差検証(Cross Validation)を利用したαの値の選定

LassoCVを使ってαの値を交差検証(Cross Validation)で推定する。
LeastAngleRegressionを使ったLassoLarsCVがあるが、より多次元データに対してはLassoCVの方が好ましいとされている。

lasso_cv = linear_model.LassoCV(alphas=[0.01,0.1, 1.0], cv=5)
lasso_cv.fit(X,y)
print(lasso_cv.alpha_)
実行結果

1.0
グラフをプロットしてみる。

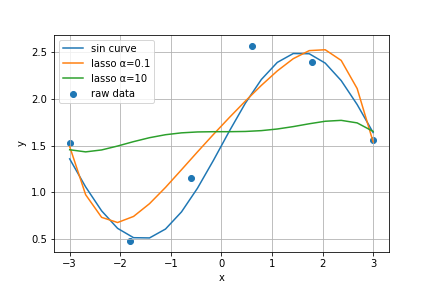
plt.scatter(X[:,0], y, label='raw data')
plt.plot(xx, np.sin(xx)+1.5, label='sin curve')
plt.plot(xx, reg_lasso.predict(XX), label='lasso α=0.1')
plt.plot(xx, lasso_cv.predict(XX), label='lasso α=10')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid()
plt.show()
実行結果
学習されたパラメータは以下の通り。
モデルw_0w_1w_2w_3w_4w_5
OLS1.9371.283-0.216-0.2820.0190.015
Lasso(α=0.1)1.710.575-0.0290.00.001-0.007
Lasso(α=1.0)1.6500.00.00.025-0.001-0.002
Ridge(α=0.5)1.740.127-0.0560.1550.003-0.018

まとめ

今回はラッソ回帰とリッジ回帰についてまとめた。
線形回帰ではかなりお世話になる変数であり、リッジ回帰はkaggleでもモデルの一部として使われることもある。シンプルながらも汎用性は高いもののようだ。
理論的にもっとよく知りたい方は以下のサイトが参考になるので見てみてほしい。
重回帰モデルの理論と実装 -なぜ正則化が必要か- satopirka
Lassoの理論と実装 -スパースな解の推定アルゴリズム- satopirka
このエントリーをはてなブックマークに追加
Pocket

「ラッソ(Lasso)回帰とリッジ(Ridge)回帰をscikit-learnで使ってみる」への1件のフィードバック

  1. ピンバック: 機械学習・AI・データサイエンスの初心者が八村塁に提言！NBAで成功するために必要なこと ｜ 父ラボ

コメントは受け付けていません。