前回、NMF(非負値行列因子分解)について理論面でのまとめをした。
今回はその内容を踏まえてPythonでの実装を行ってみる。
使うモジュールは以下の通り。
python : 3.7.4
numpy
matplotlib
1.NMFの実装
1.1 Divergenceごとの更新式の実装
1.1.1 Squared Euclidean Distance
二乗ユークリッド距離でのパラメータ更新式は以下の通り。
![]()
![]()
基本的に、足し算引き算で実装するため、簡略化して、
![]() ((分子) – (分母))
((分子) – (分母))
で実装した。
def update_matrix(X, B, W, eta=1e-3):
w_diff = eta * (np.dot(B.T, X) - np.dot(np.dot(B.T, B), W))
b_diff = eta * (np.dot(X, W.T) - np.dot(np.dot(B,W), W.T))
return b_diff, w_diff
1.1.2 Kullback-Leibler Divergence
今度はKullback-Leibler Divergence。
![]()
![]()
ここでは式が成り立つように ![]() の前に
の前に ![]() をかけることで正規化をはかった。
をかけることで正規化をはかった。
def update_matrix(X, B, W, eta=1e-3):
_X = np.dot(B, W)
w_diff_denom = B.T.sum(axis=1, keepdims=True)
b_diff_denom = W.T.sum(axis=0, keepdims=True)
w_diff = eta * W/w_diff_denom * (np.dot(B.T, X/_X) -w_diff_denom)
b_diff = eta * B/b_diff_denom * (np.dot(X/_X, W.T) - b_diff_denom)
return b_diff, w_diff
1.1.3 板倉・斎藤 Divergence
板倉・斎藤(IS) Divergence の更新式とコードは以下のようになる。
![]()
![]()
def update_matrix(X, B, W, eta=1e-3):
_X_ = X/np.dot(B,W)**2
w_diff_denom = np.dot(B.T, 1.0/np.dot(B,W))
b_diff_denom = np.dot(1.0/np.dot(B,W), W.T)
w_diff = eta * W/w_diff_denom * (np.dot(B.T, _X_) - w_diff_denom)
b_diff = eta * B/b_diff_denom * (np.dot(_X_, W.T) - b_diff_denom)
return b_diff, w_diff
1.2 学習部分の実装
とりあえず初期値を0~1の一様乱数で初期化する。
eta = 1e-3
num_iter = 1000
# X が入力。(M, N).
B = np.random.rand(M, K)
W = np.random.rand(K, N)
for i in range(num_iter):
b_diff, w_diff = update_matrix(X, B, W, eta=eta)
if b_specified:
pass
else:
B += b_diff
W += w_diff
1.3 実行コード
適当な画像を作って、それに対してNMFをかけてみた。
row = 100
col = 200
X = np.sin(np.arange(row)*0.02*np.pi).reshape(row, 1) * np.cos(np.arange(col)*0.04*np.pi).reshape(1, col) + 1.0
plt.figure(figsize=(8,5))
plt.title("Original X")
plt.imshow(X)
plt.savefig("./org_X.png")
plt.close()
これを表示させてみると、以下のような画像が表示される。
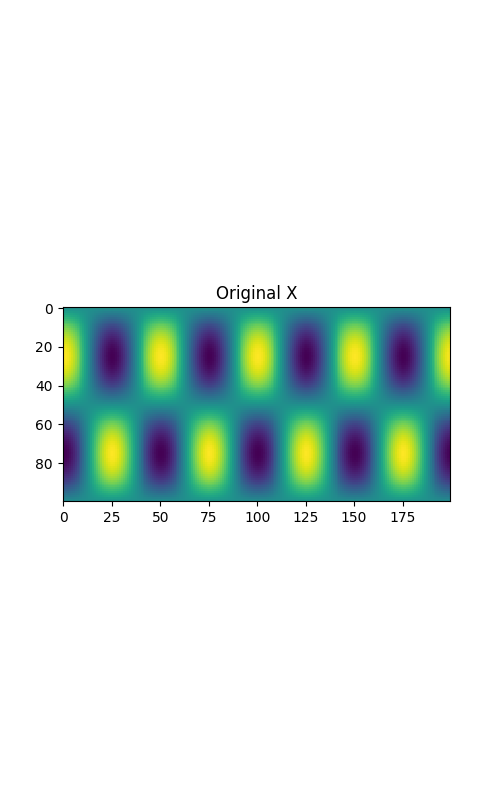
では、これらを先ほど作った3つの指標を元に作った更新式でNMFを実行する。
イテレーションの回数(num_iter)と学習率(eta)の2つの値を調整した。
NMF(.) 関数部分は他の実装も含めて記事の最後に掲載する。
for mode in ["EU", "KL", "IS"]:
if mode == "EU":
num_iter = 1000
eta = 1e-3
elif mode == "KL":
num_iter = 10000
eta = 1e-2
elif mode == "IS":
num_iter = 10000
eta = 1e-2
B, W = NMF(X, K=5, divergence=mode,
num_iter=num_iter,
eta=eta)
plt.figure(figsize=(10,8))
plt.subplot(2,1,1)
plt.title("Original X")
plt.imshow(X)
plt.subplot(2,1,2)
plt.title(f"Reconstructed with {mode}")
plt.imshow(np.dot(B, W))
plt.savefig(f"./{mode}_NMF.png")
plt.close()
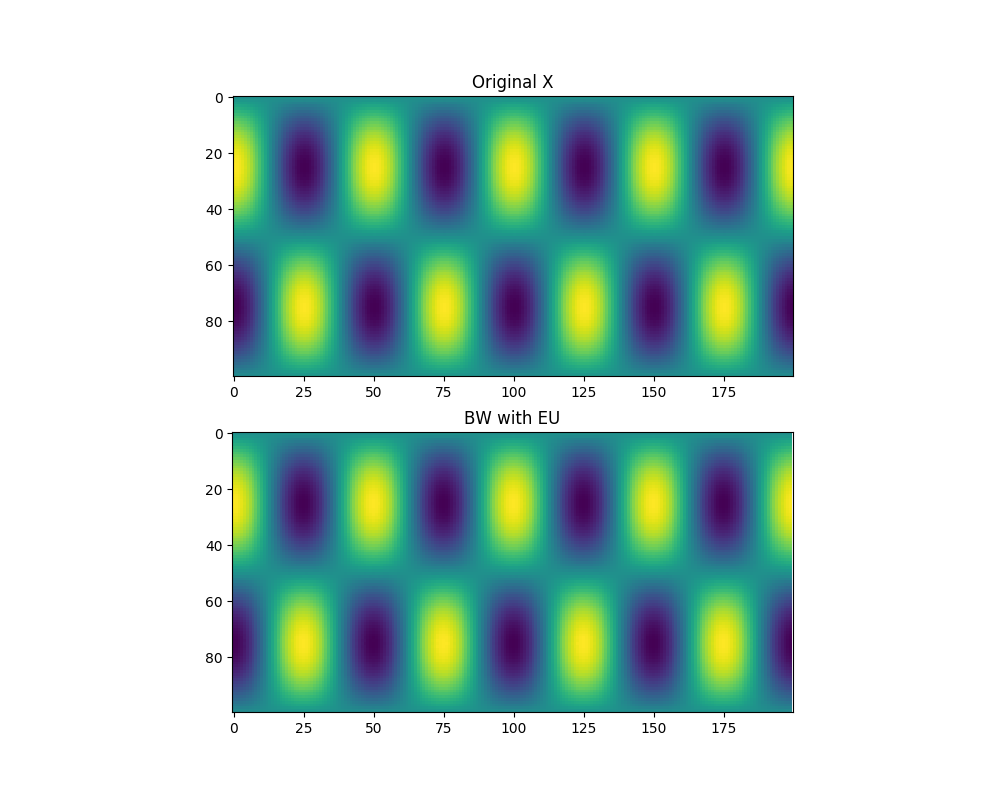
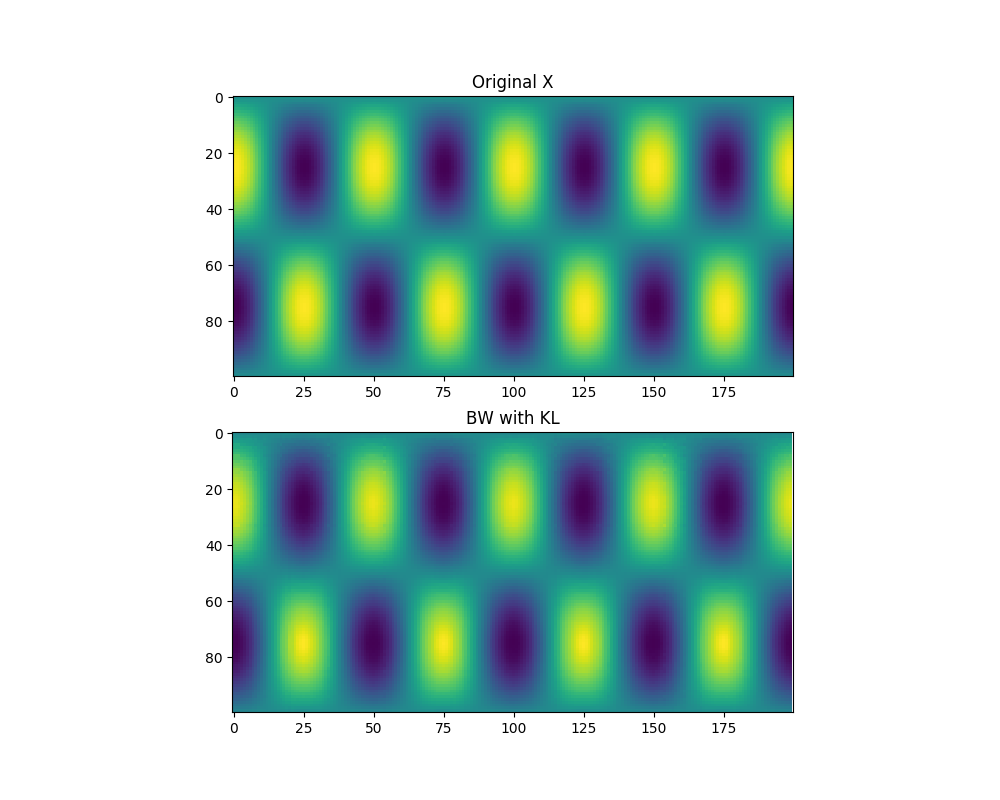
再構築された画像はそれぞれ以下のようになる。
- Euclidean Distance
- Kullback-Leibrer Divergence
- 板倉・斎藤 Divergence
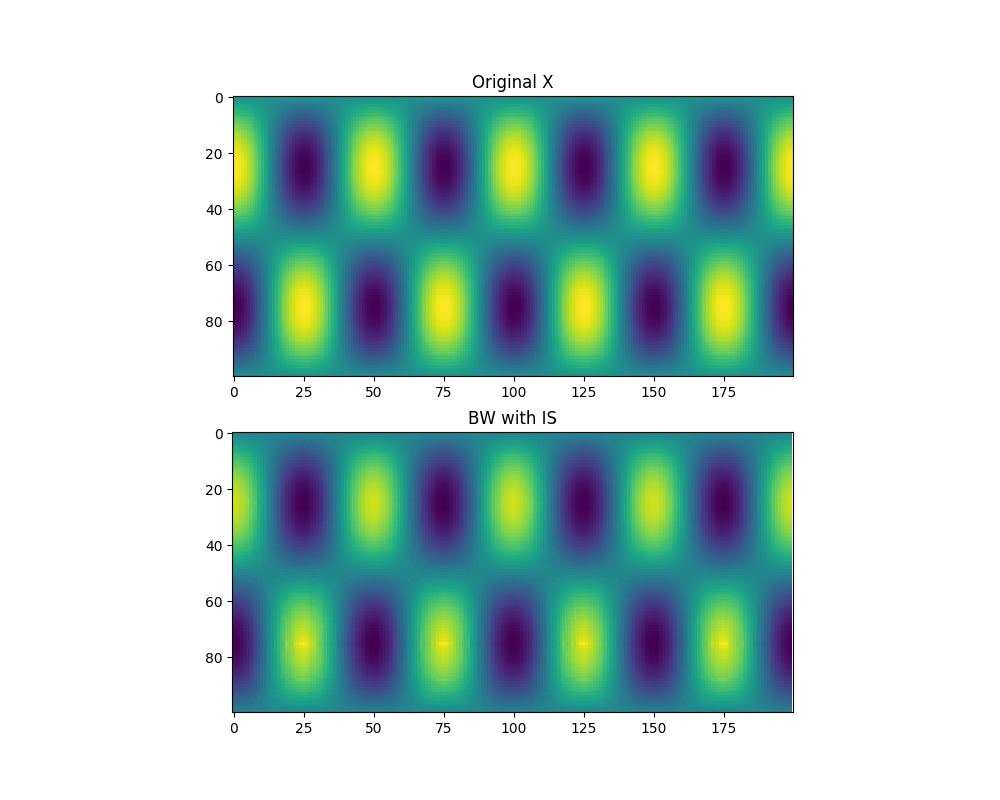
これくらい単純な画像であればどの評価指標でもまあまあうまくいくらしい。
まとめ
今回はNMFについてPythonで実装をしてみた。
色々な解析で使えるようにコードを整えておけると良いなと思った。
今度は音源分離をやってみたい。
Appendix
最後に、今回実装したコードは以下のレポジトリにアップロードした。